Public-key Encryption

What is public-key encryption

definition & history

Each party has a pair($K$, $K^{-1}$) of keys:

1. $K$ is the public key, and used for encryption
2. $K^{-1}$ is the private key, and used for decryption
3. Satisfies $D_{K^{-1}}[E_K[M]]=M$

Secure Public Key encrytion is impossible when P=NP.(ref NP Theory)

Proposed by Diffie and Hellman, documented in "New Directions in Cryptography" (1976):

• Public-key encryption schemes
• Key distribution systems
• Digital signature

public key encryption algorithm

• RSA: based on the hardnesss of factoring large numbers
• EIGamal: based on the hardness of solving discrete algorithm

Diffie-Hellman Key Agreement Protocol

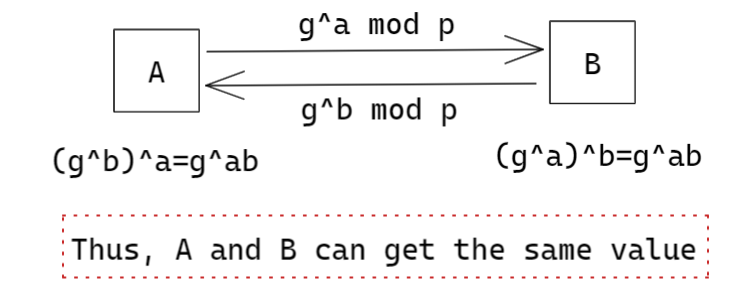
Security of DH is based on Three Hard Problems

1. Discrete Log Problem(DLG)
2. Computational Diffies Hellman Problem(CDH)
3. Decision Diffie Hellman Problem(DDH)

EIGamal Encryption

• Public Key$<g,p,h=g^a\mathrm{m}\mathrm{o}\mathrm{d}p>$
• Private key is $a$
• To encrypt message $M$: choose random $b$, computes $C=[g^b\mathrm{m}\mathrm{o}\mathrm{d}p,g^{ab}\cdot M\mathrm{m}\mathrm{o}\mathrm{d}p]$
• To decrypt message $M$: $((c_1{)}^a\mathrm{m}\mathrm{o}\mathrm{d}p)\cdot M=c_2$, find $t$ which satisfies $(c_1{)}^p\cdot t=1$, thus $M=c_2\times t$

RSA Algorithm

Invented in 1978 by Ron Rives, Adi Shamir and Leonard Adleman

Key generation

1. Select 2 large prime numbers of about the same size, p and q
2. Compute $n=pq$, and $\mathrm{\Phi }(n)=(q-1)(p-1)$
3. Select $e$, $1<e<\mathrm{\Phi }(n)$, $e$ and $\mathrm{\Phi }(n)$ are coprime
4. Determine $d$ as $d\equiv e^{-1}$ (mod $\lambda (n)$)

Encryption

$c\equiv m^e(\mathrm{m}\mathrm{o}\mathrm{d}n)$

Decryption

$c^d\equiv (m^e{)}^d\equiv m(\mathrm{m}\mathrm{o}\mathrm{d}n)$

RSA security

• the length of $n=pq$ reflects the strength
• Factoring is easy to break with quantum computers
• plain RSA does not provide IND-CPA security

Usage

• Often used to encrypt a symmetric key
• Signature(reverse usage)

ECC Algorithm

Digital Signatures

definition

signatures provide non-repudiation

• MAC: One party generated MAC, one party verifies integrity(one to one)
• Digital signatures: One party generates signature, many parties can verify(one to many)
• Digital signature scheme
  • a signing algorithm: takes a message and a (private) signing key, outputs a signature.
  • a verification algorithm: takes a (public) verification key, am essage and a signature.
• It provides
  • Authentication
  • Data integrity
  • Non-Repudiation

RSA Signatures

• Public key(e, n): used for verification
• Private key(d): used for generation